Ukkonen 的后缀树算法的清晰解释

原文出处：http://www.oschina.net/translate/ukkonens-suffix-tree-algorithm-in-plain-english

英文原文：Ukkonen’s suffix tree algorithm in plain English?

本文试图描述Ukkonen的后缀树算法，首先叙述当字符串很简单(即不包含任何重复的字符)时的算法，然后扩展到完整的算法。

先来看一些前言：

1. 我们将要构建的，基本上像一个搜索trie结构（单词查找树）,有一个根节点，从根节点引出新的节点，以及进一步从新节点引出其它节点，依次类推。
2. 但是与搜索单词查找树不同，边标签不是单个字符。相反,每个边的标签是使用一对指针[从哪,到哪]。也可以是字符在字符串中的索引值。可以说，每个边可以标记任意长度的字符串，而只需要O(1)的空间(两个指针)。

基本原理

我想首先展示如何创建一个特别简单的字符串的后缀树，这个字符串没有重复的字符，如：

abc

这个算法从左到右按步运行。字符串的每个字符都需要一个步骤。每一步都可能涉及到多个操作,但是我们将会看到(见结尾的总结)总的复杂度是O(n)。

所以我们从最左边的字符开始，首先创建一个从根节点(在左边)到一个叶节点的边，以向树中插入单个字符“a“，并为该条边添加标签[0,#]，这表示，这条边所代表的子串从位置0开始，结束在当前的结尾。我使用符号#来表示当前末尾，现在是在位置1(a之后的右边)。（译注：当前末尾是指当前已经处理过的子串的末尾）

现在，我们拥有一棵起始树，这棵树看起来如下：

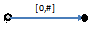
而其意义如下：

现在我们前进到位置2(b的右边）。 我们每步的目标是插入从开始位置到当前位置的子串的所有后缀。
我们通过以下动作完成目标：

•  扩展已存在边a为ab
•  插入一条新边b

按照我们的表示方法，它看起来如下：

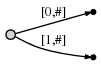
而其意义如下：

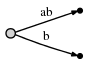
我们看到了两点：

• 表示ab的边与它在起始树的时候是相同的：[0,#]。它的意义却已经自动更改了，因为我们把当前位置#从1更改到2。

• 每条边使用的空间复杂度为O(1),因为无论边代表多少个字符 ，它都是由指向文本里的两个指针组成。

接着我们再次向右移动，并且修改树：给每个已经存在的边增加字符c，并插入一条表示新后缀c的边。
按照我们的表示方法，它看起来如下：

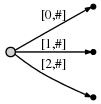
而其意义如下：

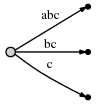
我们看到：

•   经过上面的每个步骤后，这棵树就是从起始位置到当前位置的子串的后缀树。

•   步骤数目与文本的字条相同。

•   每个步骤的工作量是O(1)，因为所有已经存在的边都是增加#来自动更改的，而且为最后一个字符插入一条新边的时间复杂度为  O(1)。因此对一个长度为n的字符串来说，只需要O(n)时间复杂度。

第一次扩展：简单的重复

当然，到目前为止后缀树工作得很好，因为我们的字符串没有包含任何重复。现在我们看一个更真实的字符串：

abcabxabcd

这个字符串由上个例子中的abc开始，接着重复ab ，紧跟着x，再接着重复abc，紧跟着d。

步骤1到3：经过了前三个步骤后，我们拥有了前面例子的那棵树：

步骤4：我们移动#到位置4。这隐含地更改所有已经存在的边为如下：

而且我们需要在根节点插入当前步骤的最末的后缀a。
我们做这些之前，我们引入除#之外的 两个或者更多变量，当然这些变量一直都存在，只是我们迄今为止没有使用它们：

•    活动点，它是一个三元组（活动节点，活动边，活动长度）

•    剩余后缀数，它是一个整数，来说明我们需要插入多少个新的后缀。

这两个变量的确切含义不久就会清晰，不过现在我们只能说：

•  在简单的abc例子里，活动点总是(root,’0x’,0),也就是说，活动节点是根节点，活动边是由空字符’0x’指定的边，活动长度是0。根节点作为活动点的结果是我们在每一步骤里需要创建新的边并插入到根节点。不久我们就会明白为什么需要三元组表示这条信息。
•  在每个步骤开始时剩余后缀数总是设置为1。它的意义是我们在每一步骤末尾时需要主动插入的后缀数目是1（总是最后一个字符）。

现在将有变化了，当我们给根节点插入当前最后一个字符a的时候，我们特别注意到已经存在一条以a开始的边：abca。在这种情况下我们做如下工作：

• 我们不向根节点插入一条新边[4,#]。相反，我们只是注意到后缀a已经在我们的树里。它终止在更长的边的中间位置，不过这么做我们并不疑惑，我们还是保留它们原来的样子。

• 我们设置活动点为(root,’a’,1)。这意味着活动点现在是在根节点的以a开始的向外的边的中间某个位置，具体地指这条边的位置1之后。我们注意到这条边只是由它的首个字符a来声明的。这就足够了，因为以一个特定的字符开始的只有一条边（通读整个文档之后可以确定这是真的）。

• 我们还增加了剩余后缀数， 那么在下一步骤开始的时候，剩余后缀数为2。

注意：当发现我们需要插入的最终后缀已经存在在这棵树里的时候，这棵树本身根本就没有改变（我们只是修改了活动节点和剩余后缀数）。那么这棵树就不再是能准确的表示至当前位置的后缀树了，不过它包含了所有的后缀（因为最终的后缀a隐含地包含了）。因此，除了修改变量外（所有这些变量都是定长的，因此空间复杂度是 O(1)），在这一步里没有做其他工作。

步骤5：我们修改当前的位置#为5。这将自动地如下更新这棵树：

而且 由于剩余后缀数为2 ，我们需要插入目前位置的两个最终后缀：ab和b。这主要是因为：

• 前一步骤的a后缀从来都没有真正地插入。因此它保留下来，然而由于我们已经向前走了一步，它现在由a延长为ab。

•  还有，我们需要插入新的最终边b。

实际上，这意味着我们要修改活动点（它现在指向的是abcab边里的a之后），而且插入当前的最后一个字符b， 不过：同时它也证明b也 已经出现在同一条边里。
因此，我们再次不修改这棵树，我们只是：

•  修改活动点为(root,’a’,2)(是与前面相同的节点和边，只不过现在我们指向到b之后)

•  增加剩余后缀数为3 ，因为我们仍然不能插入前一个步骤的最终边，同时我们也不能插入当前的最终边

为了清晰地说明：我们需要在当前的步骤里插入ab和b，不过由于ab已经找到，所以我们修改了活动点，而且甚至不试图插入b。为什么？因为如果ab处于这棵树里，那么它的每个后缀（包括b)也一定在这棵树里。也许仅仅是隐含性的，不过它一定在这棵树里，因为这是我们迄今为止建立这棵树所采用的方法。

我们增加#而前进到步骤6。这棵树自动修改为：

由于剩余后缀数是3 ，我们不得不增加abx,bx和x。活动点告诉我们ab结束在哪儿，因此我们仅仅需要跳过这儿，然后插入x。x确实还不在这棵树里，因此我们分割abcabx边，插入一个内部节点：

这条边表示的仍然是指向文本内部的指针，因此分割和插入内部节点的时间复杂度为O(1)。

这时我们处理了abx,并且把剩余后缀数减为2。现在我们需要插入下一个剩余后缀bx。但是在我们做这些之前，我们需要修改活动节点。分割并插入一条边遵循的规则称作规则1，如下，而且它适用于活动节点是根节点的情况（针对下面后续的其他情况，我们将要了解规则3）。规则1如下：

向根节点插入遵循：

• 活动节点保留为根节点
• 设置活动边为我们需要插入的新后缀的第一个字符，也就是b。
• 活动长度减1

因此，新的活动节点三元组(root,’b’,1)表明要做的下一个插入在bcabx边，第一个字符之后，即b之后。我们可以确定插入点的时间复杂度为 O(1)，并且检查x是否已经出现在树里。如果它出现在这条边里，我们将结束当前的步骤，保持一切为原样。然而如果x没有出现在这条边里，那么我们分割这条边而插入它：

再此说明，它的时间复杂度为 O(1)，而且我们按照规则1所示把剩余后缀数修改为1，活动节点修改为(root,’x’,0)。

不过还有一件事情我们必须做。我们称它为规则2：

如果我们分割一条边并插入新的节点，而且如果它不是在当前步骤里创建的第一个节点
的话，我们通过特殊的指针，即后缀连接，把 以前插入的节点和新增的节点连接起来
。后面我们将明白为什么这么做是有用的。这儿我们要明白：后缀连接表示为虚线边：

我们仍然需要插入当前步骤的最终后缀x。因为活动节点的活动长度部分已经减少到0，最终直接插入到根节点上。由于根节点上没有以x开始的边，所以我们插入了新边：

正如你所能看到的，在当前的步骤里插入了所有剩余的后缀。

我们设置#=7而前进到步骤7，这将像往常一样自动添加下一个字符a到所有的叶子边上。然后我们试图插入新的最终字符到活动节点（根节点），然后发现它已经存在在这棵树里了。因此我们结束当前的步骤，不插入任何边，并且修改活动点位(root,’a’,1)。

设置#=8进入步骤8,我们添加b,像以前所看到的，这仅仅意味着我们修改活动点位(root,’a’,2) ,而且不需要做其他事情就增加剩余后缀数。因为b已经出现在这棵树里。然而我们（在 O(1)时间复杂度里）注意到活动节点现在是一条边的结尾。我们通过重置活动节点位(node1,’\0x’,0)来体现这个。这儿，我们用node1来指ab边结束的哪个内部节点。

接着设置#=9进入步骤9，我们需要插入’c’,这将有助于我们理解的最后一条技巧：